Published on : 5th Oct 2021

Graph and its representation in python
Graph :
A graph is a set of vertices and edges. It is represented as G=(V, E).
Types of graph :
Based on edge :
- Directed graph
- Undirected graph
Note : When we say graph, we basically say undirected graph.
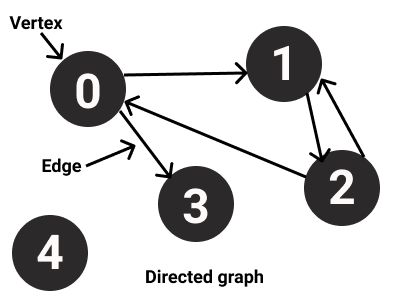
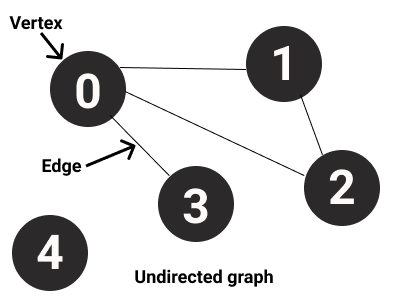
Based on weight :
- Weighted graph
- Unweighted graph
Note : When we say graph, we basically say unweighted graph.
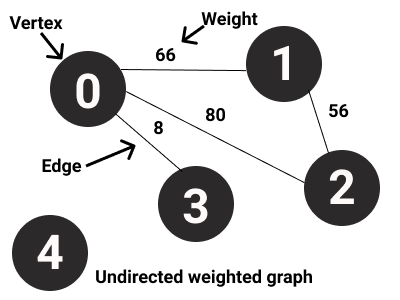
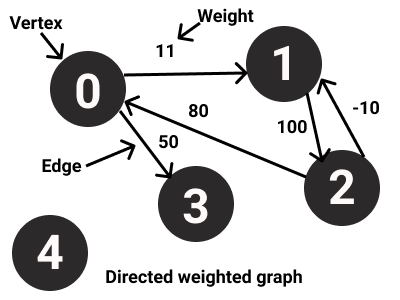
How can we represent a graph ?
- Adjacency matrix
- Adjacency list
- Edge list
Let's discuss them one by one for unweighted graph.
1. Adjacency matrix :
Explanation :
If there is an edge between src to dest vertices, we put 1 in the adjacency matrix otherwise 0.
Source code :
class Graph: def __init__(self, V, is_directed): self.V = V self.is_directed = is_directed self.adj_mat = [[0 for col in range(self.V)] for row in range(self.V)] def add_edge(self, u, v): self.adj_mat[u][v] = 1 if not self.is_directed: self.adj_mat[v][u] = 1 def print_graph(self): print("\nAdjacency matrix: ") for u in range(self.V): for v in range(self.V): print(self.adj_mat[u][v], end="\t") print() def main(): V = int(input("Enter the no. of vertices: ")) E = int(input("Enter the no. of edges: ")) is_directed = bool(int(input("is the graph directed? Enter 1 if yes otherwise 0: "))) graph = Graph(V, is_directed) for e in range(E): u, v = list(map(int, input(f"Enter src and dist vertices respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v) graph.print_graph() if __name__ == '__main__': main()
Output :
Enter the no. of vertices: 5 Enter the no. of edges: 4 is the graph directed? Enter 1 if yes otherwise 0: 0 Enter src and dist vertices respectively for edge 1: 0 1 Enter src and dist vertices respectively for edge 2: 0 2 Enter src and dist vertices respectively for edge 3: 0 3 Enter src and dist vertices respectively for edge 4: 1 2 Adjacency matrix: 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0
2. Adjacency list :
Explanation :
Here, we represent graph as hashmap. If there is an edge between src to dest, we create a linked list from src to dest. If the linked list exists started by src, then we just add dest node to the linked list.
Source code :
class Graph: def __init__(self, V, is_directed): self.V = V self.is_directed = is_directed self.adj_list = {u : [] for u in range(self.V)} def add_edge(self, u, v): self.adj_list[u].append(v) if not self.is_directed: self.adj_list[v].append(u) def print_graph(self): print("\nAdjacency list: ") for u in range(self.V): print(u, end=" ") for v in self.adj_list[u]: print("-->", v, end=" ") print() def main(): V = int(input("Enter the no. of vertices: ")) E = int(input("Enter the no. of edges: ")) is_directed = bool(int(input("is the graph directed? Enter 1 if yes otherwise 0: "))) graph = Graph(V, is_directed) for e in range(E): u, v = list(map(int, input(f"Enter src and dist vertices respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v) graph.print_graph() if __name__ == '__main__': main()
Output :
Enter the no. of vertices: 5 Enter the no. of edges: 4 is the graph directed? Enter 1 if yes otherwise 0: 0 Enter src and dist vertices respectively for edge 1: 0 1 Enter src and dist vertices respectively for edge 2: 0 2 Enter src and dist vertices respectively for edge 3: 0 3 Enter src and dist vertices respectively for edge 4: 1 2 Adjacency list: 0 --> 1 --> 2 --> 3 1 --> 0 --> 2 2 --> 0 --> 1 3 --> 0 4
3. Edge list :
Explanation :
Here, we represent graph as a list of edges.
Source code :
class Graph: def __init__(self, V, is_directed): self.V = V self.is_directed = is_directed self.edge_list = [] def add_edge(self, u, v): self.edge_list.append([u, v]) if not self.is_directed: self.edge_list.append([v, u]) def print_graph(self): print("\nEdge list: ") for i, [u, v] in enumerate(self.edge_list): print(u, "-->", v, end="") if i != len(self.edge_list)-1: print(end=", ") def main(): V = int(input("Enter the no. of vertices: ")) E = int(input("Enter the no. of edges: ")) is_directed = bool(int(input("is the graph directed? Enter 1 if yes otherwise 0: "))) graph = Graph(V, is_directed) for e in range(E): u, v = list(map(int, input(f"Enter src and dist vertices respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v) graph.print_graph() if __name__ == '__main__': main()
Output :
Enter the no. of vertices: 5 Enter the no. of edges: 4 is the graph directed? Enter 1 if yes otherwise 0: 1 Enter src and dist vertices respectively for edge 1: 0 1 Enter src and dist vertices respectively for edge 2: 0 2 Enter src and dist vertices respectively for edge 3: 0 3 Enter src and dist vertices respectively for edge 4: 1 2 Edge list: 0 --> 1, 0 --> 2, 0 --> 3, 1 --> 2
Now, let's discuss for weighted graph.
1. Adjacency matrix :
Explanation :
If there is an edge between src to dest vertices, we put the weight of the edge in the adjacency matrix otherwise 0.
Source code :
class Graph: def __init__(self, V, is_directed, is_weighted): self.V = V self.is_directed = is_directed self.is_weighted = is_weighted self.adj_mat = [[0 for col in range(self.V)] for row in range(self.V)] def add_edge(self, u, v, w=0): if self.is_weighted: self.adj_mat[u][v] = w else: self.adj_mat[u][v] = 1 if not self.is_directed: if self.is_weighted: self.adj_mat[v][u] = w else: self.adj_mat[v][u] = 1 def print_graph(self): print("\nAdjacency matrix: ") for u in range(self.V): for v in range(self.V): print(self.adj_mat[u][v], end="\t") print() def main(): V = int(input("Enter the no. of vertices: ")) E = int(input("Enter the no. of edges: ")) is_directed = bool(int(input("is the graph directed? Enter 1 if yes otherwise 0: "))) is_weighted = bool(int(input("is the graph weighted? Enter 1 if yes otherwise 0: "))) graph = Graph(V, is_directed, is_weighted) for e in range(E): if graph.is_weighted: u, v, w = list(map(int, input(f"Enter src, dist vertices and weight respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v, w) else: u, v = list(map(int, input(f"Enter src and dist vertices respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v) graph.print_graph() if __name__ == '__main__': main()
Output :
Enter the no. of vertices: 5 Enter the no. of edges: 4 is the graph directed? Enter 1 if yes otherwise 0: 0 is the graph weighted? Enter 1 if yes otherwise 0: 1 Enter src, dist vertices and weight respectively for edge 1: 0 1 66 Enter src, dist vertices and weight respectively for edge 2: 0 2 80 Enter src, dist vertices and weight respectively for edge 3: 0 3 8 Enter src, dist vertices and weight respectively for edge 4: 1 2 56 Adjacency matrix: 0 66 80 8 0 66 0 56 0 0 80 56 0 0 0 8 0 0 0 0 0 0 0 0 0
2. Adjacency list :
Explanation :
We put dest vertex and weight in the linked list.
Source code :
class Graph: def __init__(self, V, is_directed, is_weighted): self.V = V self.is_directed = is_directed self.is_weighted = is_weighted self.adj_list = {u : [] for u in range(self.V)} def add_edge(self, u, v, w=0): if self.is_weighted: self.adj_list[u].append([v, w]) else: self.adj_list[u].append(v) if not self.is_directed: if self.is_weighted: self.adj_list[v].append([u, w]) else: self.adj_list[v].append(u) def print_graph(self): print("\nAdjacency list: ") if self.is_weighted: for u in range(self.V): print(u, end="") for v, w in self.adj_list[u]: print(" --> ", v, f"[{w}]", end="") print() else: for u in range(self.V): print(u, end="") for v in self.adj_list[u]: print(" --> ", v, end="") print() def main(): V = int(input("Enter the no. of vertices: ")) E = int(input("Enter the no. of edges: ")) is_directed = bool(int(input("is the graph directed? Enter 1 if yes otherwise 0: "))) is_weighted = bool(int(input("is the graph weighted? Enter 1 if yes otherwise 0: "))) graph = Graph(V, is_directed, is_weighted) for e in range(E): if graph.is_weighted: u, v, w = list(map(int, input(f"Enter src, dist vertices and weight respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v, w) else: u, v = list(map(int, input(f"Enter src and dist vertices respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v) graph.print_graph() if __name__ == '__main__': main()
Output :
Enter the no. of vertices: 5 Enter the no. of edges: 5 is the graph directed? Enter 1 if yes otherwise 0: 1 is the graph weighted? Enter 1 if yes otherwise 0: 1 Enter src, dist vertices and weight respectively for edge 1: 0 1 11 Enter src, dist vertices and weight respectively for edge 2: 1 2 100 Enter src, dist vertices and weight respectively for edge 3: 2 1 -10 Enter src, dist vertices and weight respectively for edge 4: 2 0 80 Enter src, dist vertices and weight respectively for edge 5: 0 3 50 Adjacency list: 0 --> 1 [11] --> 3 [50] 1 --> 2 [100] 2 --> 1 [-10] --> 0 [80] 3 4
3. Edge list :
Explanation :
Here, we represent graph as a list of edges along with weight.
Source code :
class Graph: def __init__(self, V, is_directed, is_weighted): self.V = V self.is_directed = is_directed self.is_weighted = is_weighted self.edge_list = [] def add_edge(self, u, v, w=0): if self.is_weighted: self.edge_list.append([u, v, w]) else: self.edge_list.append([u, v]) if not self.is_directed: if self.is_weighted: self.edge_list.append([v, u, w]) else: self.edge_list.append([v, u]) def print_graph(self): print("\nEdge list: ") if self.is_weighted: for i, [u, v, w] in enumerate(self.edge_list): print(u, "-->", v, f"[{w}]", end="") if i != len(self.edge_list)-1: print(end=", ") else: for i, [u, v] in enumerate(self.edge_list): print(u, "-->", v, end="") if i != len(self.edge_list)-1: print(end=", ") def main(): V = int(input("Enter the no. of vertices: ")) E = int(input("Enter the no. of edges: ")) is_directed = bool(int(input("is the graph directed? Enter 1 if yes otherwise 0: "))) is_weighted = bool(int(input("is the graph weighted? Enter 1 if yes otherwise 0: "))) graph = Graph(V, is_directed, is_weighted) for e in range(E): if graph.is_weighted: u, v, w = list(map(int, input(f"Enter src, dist vertices and weight respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v, w) else: u, v = list(map(int, input(f"Enter src and dist vertices respectively for edge {e+1}: ").split(' '))) graph.add_edge(u, v) graph.print_graph() if __name__ == '__main__': main()
Output :
Enter the no. of vertices: 5 Enter the no. of edges: 4 is the graph directed? Enter 1 if yes otherwise 0: 0 is the graph weighted? Enter 1 if yes otherwise 0: 1 Enter src, dist vertices and weight respectively for edge 1: 0 1 66 Enter src, dist vertices and weight respectively for edge 2: 0 2 80 Enter src, dist vertices and weight respectively for edge 3: 0 3 8 Enter src, dist vertices and weight respectively for edge 4: 1 2 56 Edge list: 0 --> 1 [66], 1 --> 0 [66], 0 --> 2 [80], 2 --> 0 [80], 0 --> 3 [8], 3 --> 0 [8], 1 --> 2 [56], 2 --> 1 [56]